Estimating the dispersion parameter¶

Here, we show how to estimate the dispersion parameter with Pastis.

import matplotlib.pyplot as plt
import numpy as np
from iced import datasets
import iced
from pastis import dispersion

Load a Yeast dataset, and a human dataset

counts, lengths = datasets.load_sample_yeast()

Out:

/usr/share/miniconda3/envs/pastis/lib/python3.9/site-packages/iced/io/_io_pandas.py:56: UserWarning: Attempting to guess whether counts are 0 or 1 based
  warnings.warn(

Normalize the contact count data, but keep the biases to estimate the dispersion

counts = iced.filter.filter_low_counts(counts, percentage=0.06)
normed_counts, biases = iced.normalization.ICE_normalization(
    counts,
    output_bias=True)

Now, estimate the variance and mean for every genomic distance

Note that in order to have an unbiased estimation of the variance, you need to provide the bias vector.

_, mean, variance, weights = dispersion.compute_mean_variance(
    counts, lengths, bias=biases)

Now, estimate a constant and a functional dispersion parameter.

cst_disp = dispersion.ExponentialDispersion(degree=0)
cst_disp.fit(mean, variance, sample_weights=weights**0.5)

fun_disp = dispersion.ExponentialDispersion(degree=1)
fun_disp.fit(mean, variance, sample_weights=weights**0.5)

Out:

<pastis.dispersion.ExponentialDispersion object at 0x7fbba9e36820>

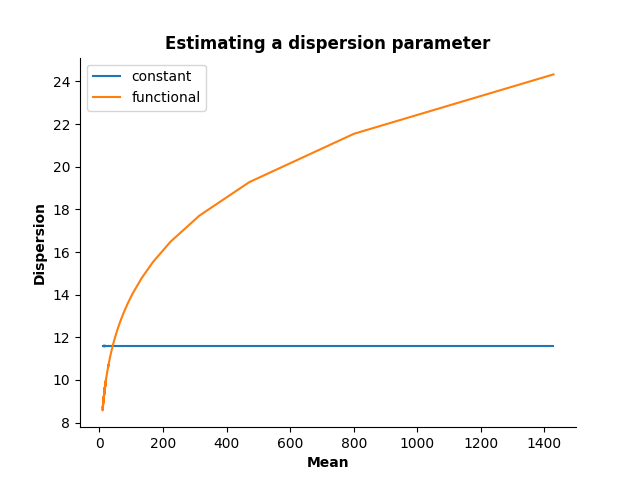
Plot the dispersion as a function of the mean

fig, ax = plt.subplots()
ax.plot(mean, cst_disp.predict(mean), label="constant")
ax.plot(mean, fun_disp.predict(mean), label="functional")
ax.legend()

ax.set_xlabel("Mean", fontweight="bold")
ax.set_ylabel("Dispersion", fontweight="bold")
ax.set_title("Estimating a dispersion parameter", fontweight="bold")
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

Total running time of the script: ( 0 minutes 0.201 seconds)

Gallery generated by Sphinx-Gallery